At Azavea, full-time software developers have the opportunity to put 10% of their time towards learning and research. I am using my 10% time to explore a pure, statically-typed functional programming language called Idris by working my way through the excellent Type-Driven Development with Idris written by Edwin Brady, the creator of the language.
The thesis of the book is that instead of trying to use tests to check for the presence of errors, we can use types to demonstrate the absence of errors in our code. Not only that, we can make types work for us by leveraging the properties of Idris and its powerful type system to help us write code. In type-driven development, we start with the types and the compiler guides us along as we implement our program.
Let’s take a look at how.
Functions
Here is a simple function signature in Idris:
add : Int -> Int -> Int
Function signatures describe a function’s inputs and outputs. In Idris, you can think of the function signature as a contract that describes exactly what the function must do. In the above example, we are defining a function named add which takes two Ints as input and returns an Int as output (Int is a built-in type representing integers):
add : Int -> Int -> Int
^^^ ^^^ ^^^
input input output
We’ll always start with a function signature and work towards the implementation from there. In this case, the implementation would look like this:
add x y = x + y
add takes two arguments x and y and we add them together using the + operator. The body of our function is an expression which evaluates to a value that is implicitly returned by the function. As such, no explicit returns are needed. We end up with this:
add : Int -> Int -> Int add x y = x + y
We can fire up an Idris REPL within the context of the Idris file we’re working in (Add.idr) by running idris Add.idr and then call our function like so (notice the lack of parentheses):
*Add> add 1 2 3 : Int
We can see from the output (3 : Int) that we got back a 3 that is of type Int.
This function, like all Idris functions, is pure. That means that the same input to the function must produce the same output and the function can have no side effects (nothing besides returning a value). In short, pure functions are dependable and predictable. They can always be relied on to do exactly what they say and nothing more; they won’t fetch data from a server, mutate some global state, launch a rocket into the sun, or any other shenanigans.
As we will see later, this property of purity will be leveraged extensively by the compiler to not only make sure our programs are correct, but also to help us write them!
Types
You can think of types as a description of how data should be used. When practicing type-driven development in Idris, our function definitions flow from the function signature and the types contained within them. The function signatures are more than just documentation enforced by the compiler — they’re a starting point for our implementation.
Let’s start with a very simple example:
invert : Bool -> Bool
We want to write a function that will take a Bool and return a Bool (note that types in Idris must start with a capital letter). The Bool type is defined using the data keyword like so:
data Bool = False | True
Bool is a union type that can be either True or False. Thus, our invert function should switch between these two possibilities (True becomes False and False becomes True).
Now, to help us code in Idris, there are plugins available for common text editors such as Vim, Emacs, and Atom which provide a set of standard commands to facilitate type-driven development. To start, we can use the definition command (<LocalLeader>d in Vim) to build out an initial function definition:
invert : Bool -> Bool invert x = ?invert_rhs
We see that Idris has started implementing this function for us and already has added an x argument for our function equation. Cool!
But what about the ?invert_rhs? That is called a type hole. A type hole always starts with a question mark and represents a yet-to-be-implemented part of your program. If we check the type of our type hole (<LocalLeader>t in Vim) using the plugin we see this output:
x : Bool -------------------------------------- invert_rhs : Bool
That’s telling us that x is a Bool and invert_rhs (the expression our function body evaluates to) is too, as we would expect.
Next we can use the case-split command (<LocalLeader>c in Vim) to continue implementing the function. By case-splitting on the argument, we get:
invert : Bool -> Bool invert False = ?invert_rhs_1 invert True = ?invert_rhs_2
Idris has helpfully leveraged what it knows about Bool and filled in the possible values for the implementation of our function. It has created a new function equation for each case to pattern match on. Now it’s up to us to fill in those type holes to complete our function:
invert : Bool -> Bool invert False = True invert True = False
Here’s how the function can be implemented start-to-finish using interactive editing:

invert function using interactive editingWe can run the function like so:
*Invert> invert True False : Bool *Invert> invert False True : Bool
Runtime Errors
If you’re not used to static typing, you may at this point be wondering what might happen if you gave invert the wrong type, something that’s not a Bool. For example, let’s try to apply invert to "banana" (a String instead of a Bool):
invert : Bool -> Bool invert False = True invert True = False result : Bool result = invert "banana"
We get this compilation error:
|
6 | result = invert "banana"
| ~~~~~~~~~~~~~
When checking right hand side of result with expected type
Bool
When checking an application of function Main.invert:
Type mismatch between
String (Type of "banana")
and
Bool (Expected type)
This is not valid Idris code; it does not compile and we can’t run it since it did not pass type checking. This is actually a good thing since the compiler won’t let us write incorrect code and thus catches many errors during development before they can become bugs.
One of the great things about static typing is that you’ll never have to write a test for what happens if your function gets or returns the wrong type because it simply can’t happen — it would be impossible to write a test case like that because it wouldn’t compile! The more powerful the type system, the more precisely we can define our types and the more errors we can prevent at runtime. And as we will continue to see, Idris’s type system is quite powerful!
Defining Custom Types
We can of course define our own types based on our needs. In this example we are going to encode a simple AST in Expr for evaluating mathematical expressions which supports a few simple operations: addition, subtraction, and multiplication.
data Expr = Val Int
| Multiply Expr Expr
| Add Expr Expr
| Subtract Expr Expr
This type is recursive, meaning it is defined in terms of itself (as such, expressions can be nested). We have types for our three binary operations we have represented (addition, subtraction, and multiplication) with the constructors Add, Subtract, and Multiply, respectively, as well as Val to hold our integer literals.
Let’s examine Expr more closely in the REPL using :doc which will show the documentation for any function or type:
*Expr> :doc Expr
Data type Main.Expr : Type
Constructors:
Val : Int -> Expr
Multiply : Expr -> Expr -> Expr
Add : Expr -> Expr -> Expr
Subtract : Expr -> Expr -> Expr
We can see that Expr is in fact a Type, whereas Val, Multiply, Add, and Subtract are constructors for that type, meaning that they are simply functions that return an Expr. Notice that we didn’t have to actually write any documentation; Idris knows this about Expr by virtue of the type definition.
Let’s look at some examples to see how we could use Expr. We can represent the value 4 by itself like so:
*Expr> Val 4 Val 4 : Expr
And 4 * 2 like so:
*Expr> Multiply (Val 4) (Val 2) Multiply (Val 4) (Val 2) : Expr
And 4 * (2 - 1) like so:
*Expr> Multiply (Val 4) (Subtract (Val 2) (Val 1)) Multiply (Val 4) (Subtract (Val 2) (Val 1)) : Expr
Notice the type in all of these examples is Expr.
Now let’s write a function to evaluate our Expr with the following signature:
evaluate : Expr -> Int
Using our handy plugin, let the compiler be our guide! Running the definition command gives us:
evaluate : Expr -> Int evaluate x = ?evaluate_rhs
And case-splitting on our x argument gives us:
evaluate : Expr -> Int evaluate (Val x) = ?evaluate_rhs_1 evaluate (Multiply x y) = ?evaluate_rhs_2 evaluate (Add x y) = ?evaluate_rhs_3 evaluate (Subtract x y) = ?evaluate_rhs_4
Once we finish fleshing out our implementation by filling in the type holes, we get this:
evaluate : Expr -> Int evaluate (Val x) = x evaluate (Multiply x y) = evaluate x * evaluate y evaluate (Add x y) = evaluate x + evaluate y evaluate (Subtract x y) = evaluate x - evaluate y
We can now use our evaluate function to evaluate the examples shown earlier:
*Expr> evaluate (Val 4) 4 : Int *Expr> evaluate (Multiply (Val 4) (Val 2)) 8 : Int *Expr> evaluate (Multiply (Val 4) (Subtract (Val 2) (Val 1))) 4 : Int
This shows the process of implementing the function using interactive editing:
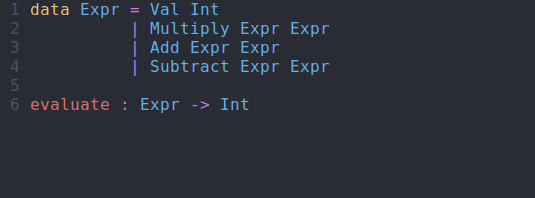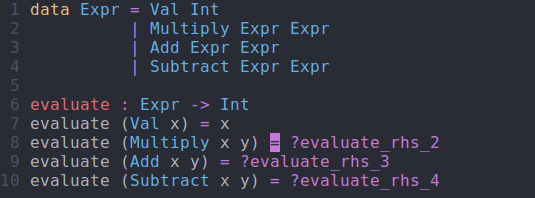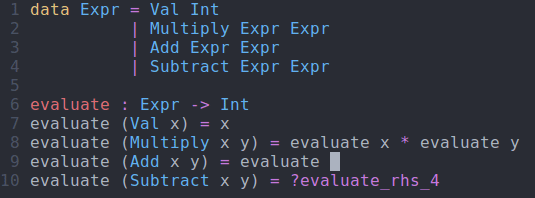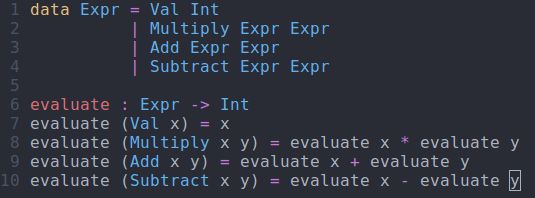
evaluate function using interactive editingModifying Our Code
Let’s say we want to add a new operation to our program: division. This will require a change to our Expr type:
data Expr = Val Int
| Multiply Expr Expr
| Add Expr Expr
| Subtract Expr Expr
| Divide Expr Expr
Immediately the compiler lets us know of a potential problem:
| 8 | evaluate (Val x) = x | ~~~~~~~~~~~~~~~~~~~~ Main.evaluate is not total as there are missing cases
The error message indicates that the compiler is looking for our evaluate function to account for the possible input of Divide x y. This is because Idris enforces totality, an even stronger property than purity. A total function is guaranteed to produce an output for any well-typed input in finite time, and a function is assumed to be total unless it is explicitly annotated as a partial function using partial. This means that we are forced to account for all possible inputs, which we are not doing in this case.
To make our function total, we can modify evaluate like so:
evaluate : Expr -> Int evaluate (Val x) = x evaluate (Multiply x y) = evaluate x * evaluate y evaluate (Add x y) = evaluate x + evaluate y evaluate (Subtract x y) = evaluate x - evaluate y evaluate (Divide x y) = evaluate x / evaluate y
However, once we do so we see another compiler error:
|
12 | evaluate (Divide x y) = evaluate x / evaluate y
| ~~~~~~~~~~~~~~~~~~~~~~~
When checking right hand side of evaluate with expected type
Int
Can't find implementation for Fractional Int
Division is not a valid operation on Int since we cannot have fractional integers. If we replace our Int with Double our program will compile and we can use the division operator to calculate 4 / (2 - 1):
*Expr> evaluate (Divide (Val 4) (Subtract (Val 2) (Val 1))) 4.0 : Double
If we check the documentation for our function in the REPL using :doc, we see that it is total:
*Expr> :doc evaluate
Main.evaluate : Expr -> Double
The function is Total
In making this change, we see that the strong guarantees Idris affords us around type safety and totality help us avoid errors at compile time.
Generic Types
Sometimes we will want to make our types be able to take a parameter which could be of any type. For instance, the generic type List takes a type parameter elem (note that types are always UpperCamelCase whereas type parameters are always lowercase).
Observe that we can have lists of different types:
Idris> [1, 2, 3] [1, 2, 3] : List Integer Idris> ["a", "b", "c"] ["a", "b", "c"] : List String
The :: operator (pronounced “cons”) is used for adding an element to the front of a list:
Idris> 0 :: [1, 2, 3] [0, 1, 2, 3] : List Integer
The above examples use syntactic sugar that makes working with Lists easier. We can use the more verbose syntax to construct a list as well, starting with the empty list primitive Nil and using :: to build up our list backwards by glomming head elements onto it:
Idris> 0 :: (1 :: (2 :: (3 :: Nil))) [0, 1, 2, 3] : List Integer
When using syntactic sugar for lists, Idris will desugar the comma-separated elements inside of square brackets to these primitive forms.
To better understand how this works, let’s examine the List type definition:
data List elem = Nil
| (::) elem (List elem)
We can see that List is a union type of Nil (empty list) and potentially a chain of other Lists constructed via cons-ing together heads and other lists (:: is a constructor that takes a head elem and a tail List elem). Notice that all of the Lists take the same elem parameter which will necessarily be the same type.
Let’s get some practice working with Lists by implementing the takeList function (we’ll call it takeList to avoid a name conflict with the built-in take function). This function will retrieve the first n elements from a list, returning the whole list if too many elements are requested:
Idris> takeList 1 [1, 2, 3] [1] : List Integer Idris> takeList 2 [1, 2, 3] [1, 2] : List Integer Idris> takeList 3 [1, 2, 3] [1, 2, 3] : List Integer Idris> takeList 4 [1, 2, 3] [1, 2, 3] : List Integer
The function signature will look like this:
takeList : (n : Nat) -> (list : List a) -> List a
Notice that this function does not take an Int but instead takes a Nat, a natural number. This type is commonly used for working with collections in Idris since Nat must be greater than or equal to zero and collections cannot have a negative length. This is yet another example of precisely defining our types to remove potential error cases that one would otherwise need to account for.
Nat is a very simple recursive type:
data Nat = Z | S Nat
We can build up our Nat recursively starting from Z (Zero) by using S (Successor) to add to it:
Idris> Z 0 : Nat Idris> S Z 1 : Nat Idris> S (S Z) 2 : Nat
With that new knowledge of Nat in hand, let’s get back to implementing our takeList function, starting with the function signature:
takeList : (n : Nat) -> (list : List a) -> List a
You’ll notice that our function arguments look a little different than what we’ve seen up until this point. This function signature provides names for its arguments. Our first argument of type Nat is called n and our second argument of type List a is called list. As we will soon see, these names are used for better variable naming when code is generated via interactive editing.
Again using our plugin, let’s first build out an initial definition:
takeList : (n : Nat) -> (list : List a) -> List a takeList n list = ?takeList_rhs
Next, we case-split on n:
takeList : (n : Nat) -> (list : List a) -> List a takeList Z list = ?takeList_rhs_1 takeList (S k) list = ?takeList_rhs_2
We know that if Nat is Z (zero), then we’re requesting zero elements and we can return an empty list, so we can fill in ?takeList_rhs_1 with [] like so:
takeList : (n : Nat) -> (list : List a) -> List a takeList Z list = [] takeList (S k) list = ?takeList_rhs_2
The core of our function logic will depend on what we do with list. Let’s case-split on the second list to see what values it might be:
takeList : (n : Nat) -> (list : List a) -> List a takeList Z list = [] takeList (S k) [] = ?takeList_rhs_1 takeList (S k) (x :: xs) = ?takeList_rhs_3
We also know that if the list we’re working with is empty, we want to return an empty list, no matter the value of k, which means that ?takeList_rhs_1 can also be an empty list, giving us:
takeList : (n : Nat) -> (list : List a) -> List a takeList Z list = [] takeList (S k) [] = [] takeList (S k) (x :: xs) = ?takeList_rhs_3
The type hole ?takeList_rhs_3 is all that remains to be implemented. In the function equation on the last line of our implementation, we’re using the cons operator to pattern match on the head and tail (x and xs) of our list so we can work with them. By matching using ::, we not only access the head and tail but also assert that there is a head and tail to match on.
To build out the result that will be returned, we want to grab the head and then continue taking the remaining k elements from the rest of our list:
takeList : (n : Nat) -> (list : List a) -> List a takeList Z list = [] takeList (S k) [] = [] takeList (S k) (x :: xs) = x :: takeList k xs
Here is how this can be implemented with interactive editing:

takeList via interactive editingWhile this function works great on lists, in Idris we can do one better. By using a more precise collection type, we can write a takeList function where you cannot request more elements than exist in the collection and have this be enforced at compile time. Seem impossible? That’s the power of dependent types!
Dependent Types
Idris makes it possible to define types that are computed from some other value. These are called dependent types. Vect is an example of a dependent type: its length is part of its type and can therefore be checked at compile time. To put it another way, the type of Vect depends on its length. Whereas generics have a type specified as a type parameter, dependent types depend on a value being specified to determine their type.
Here is an example of a Vect:
import Data.Vect fourInts : Vect 4 Int fourInts = [1, 2, 3, 4]
This Vect has a length of 4 and is made up of Ints. If we look at the type of Vect in a REPL using :t we see:
> :t Vect Vect : Nat -> Type -> Type
Vect takes a Nat which defines its length explicitly and a Type for the type of element contained within it and returns a new Type. This is a distinctive property of Idris: types are first-class. That means we can pass them into and return them from functions. This property is important for making dependent types possible.
In the case of Vect, crucially, a Vect 4 Int is a different type than Vect 5 Int.
Let’s get some practice working with dependent types by writing a takeVect function that operates on Vects. As usual, we start with the function signature:
takeVect : (n : Nat) -> Vect (n + m) elem -> Vect n elem
This function signature looks different than others we’ve seen so far, specifically the second argument: Vect (n + m) elem. This is saying that the Nat used to construct the Vect is greater than or equal to n (since m can be greater than or equal to zero).
To start implementing our function, first we use the definition command:
takeVect : (n : Nat) -> Vect (n + m) elem -> Vect n elem takeVect n xs = ?takeVect_rhs
Followed by case-splitting on n:
takeVect : (n : Nat) -> Vect (n + m) elem -> Vect n elem takeVect Z xs = ?takeVect_rhs_1 takeVect (S k) xs = ?takeVect_rhs_2
Next we can use the search command (<LocalLeader>o in Vim) to search for an expression that satisfies the type hole:
takeVect : (n : Nat) -> Vect (n + m) elem -> Vect n elem takeVect Z xs = [] takeVect (S k) xs = ?takeVect_rhs_2
In this case, Idris was able to fill in the expression for us since when n is zero, we necessarily must have an empty Vect. The last remaining step is to implement ?take_rhs_2 similarly to how it was done for takeList:
takeVect : (n : Nat) -> Vect (n + m) elem -> Vect n elem takeVect Z xs = [] takeVect (S k) (x :: xs) = x :: takeVect k xs
This shows the process of implementing our function:
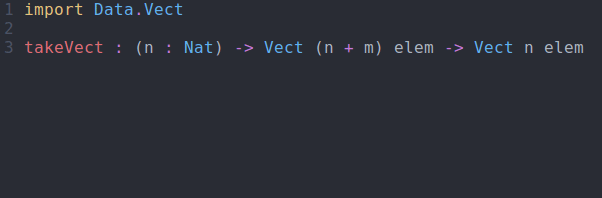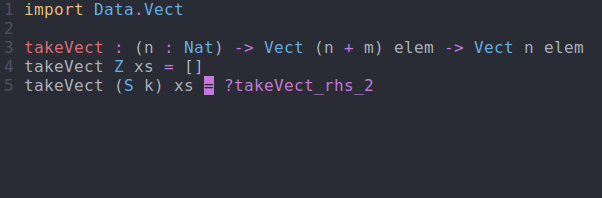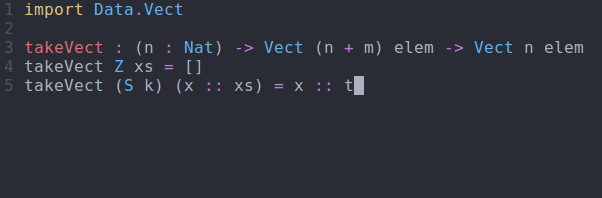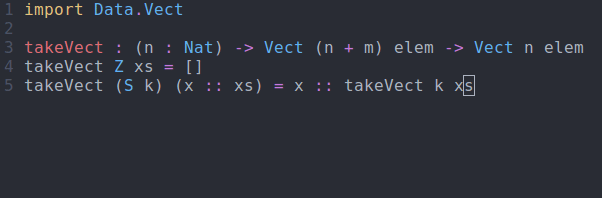
takeVect via interactive editingSo what does this get us? Well, if we try to take more elements than are available, we get a compile time error:
*Take> takeVect 5 [1, 2, 3, 4]
(input):1:13:When checking argument xs to constructor Data.Vect.:::
Type mismatch between
Vect 0 elem1 (Type of [])
and
Vect (S m) elem (Expected type)
Specifically:
Type mismatch between
0
and
S m
As we can see, by crafting our function signatures correctly, we can leverage the power of dependent types to make invalid operations impossible and have that be enforced at compile time.
Conclusion
As we have seen, instead of using types to check for correctness after the fact, they can be the starting point for your programs. In Idris, your functions flow from your types with the compiler as your guide. By precisely defining our types, once the code has compiled successfully, we can be reasonably confident that it is working as intended. And any future changes can be made knowing that the compiler has you covered.
Though Idris is primarily a research language and is not yet ready for production, the ideas behind it are compelling. Dependent types have many potentially interesting applications to aid in writing correct programs beyond the examples already shown, such as money being dependent on time. As an example in a geospatial context, we could imagine using dependent types to ensure map algebra operations are only performed on rasters with the same CRS and resolution.
Type-driven development is a powerful way to write correct programs, and what’s shown here is only a taste of what Idris has to offer. To learn more, check out the Idris docs or pick up a copy of Type-Driven Development with Idris.
